NP Hard and NP Complete Problems

NP-Hard: If every problem in NP can be polynomial time reducible to a problem ‘A’, then ‘A’ is called NP-Hard. If ‘A’ could be solved in polynomial time then every problem in NP is ‘P’. For example. arm wrestling

P = NP, then

NP-Complete: A problem, if it is in NP and NP-Hard, then it is said to be NP-Complete problem.

In order to colve NP = P, if we take any problem from NPC and prove that we can solve it in polynomial time then P = NP, or

We take 1 NPC problem, which is meant to be already present in NP and we say that it can never be solved in polynomial time, then we have found that there is a problem which is present in NP and which is not present in P.

Note:

- If NP-Hard or NP-Complete is solved in polynomial time, then NP = P.
- If NP or NP-Complete problem is proven to be not solvable in polynomial time, then P != NP.

But, till date it is not possible to find out whether NP = P or not.

- Status of NP is still unknown.

Suppose ‘B’ is in NP, ‘A’ is in NP-Hard.

If A can be computed in polynomial time which is NP-Hard and if we are able to convert A to B in polynomial time, then B is also NP-hard.

Now, it is given that B is already in NP and it is also proved to be NP-Hard. Therefore, B is NP-Complete.

Note: To find out whether a problem is NP-Complete, we find out one problem which is known to be NP-Complete and from that problem, we give transformation to some other problem. Then, the problem will become NP-Complete.

If NP-Complete and NP-Hard problem is converted to NP problem then, the NP problem is also NP-Complete.

Problems:-

1. Circuit-satisfyiablity (CS)

Every problem in computer system is converted into digital logic form and inputs are given. If we can find out a circuit which can solve that problem and say Yes/No. So, if we have an algorithm to solve the circuit then that is the algorithm to solve that problem.

If a problem converted in digital form can be solved in polynomial time, then that problem too can be solved in polynomial time.

This is the first problem, i.e., proved to be NP-Complete problem. Example, combination of input that can result value ‘TRUE’.

2. Satisfyiablity (S)

It is nothing but a formula kind. Circuit-satisfyiability problem converted into satisfyiability problem. It is a combination of boolean variables and operators.

Examples, Is there any assignment to the variables such that it produces ‘TRUE’.

(x + y + z) . (xy) . (yz)

Therefore, CS can be converted to S in polynomial time, hence this is also NP-Complete.

As all problems in the diagram are in NP and we are converting CS into S in polynomial time. Hence, S will become NP-Hard. It is already in NP and now in NP-Hard, hence NP-Complete.

3. 3CNF-Satisfyiability (3CNF-S)

It means ‘anding’ of ‘or’ terms. It contains 3 terms. Example, (x + y + z(bar)) . (a + b(bar) + c)

Now, we can convert S into 3CNF-S, therefore 3CNF-S is also NP-Complete.

4. Clique

If there is a graph then, the maximum sub graph of the given graph which is complete, is clique.

Example,

BCED is not complete, but ABC is complete.

Therefore, clique solution is 3

5. Vertex Cover

If there is a graph given, how many vertices should we choose so that we cover all the edges.

Example,

Here, if we place or choose ‘A’ and ‘C’ then AB and AD is converted by ‘A’ and CD is converted by ‘C’. Therefore, all the edges can be converted by choosing ‘A’ and ‘C’ as vertices. Therefore, this is also NP-Complete problem.

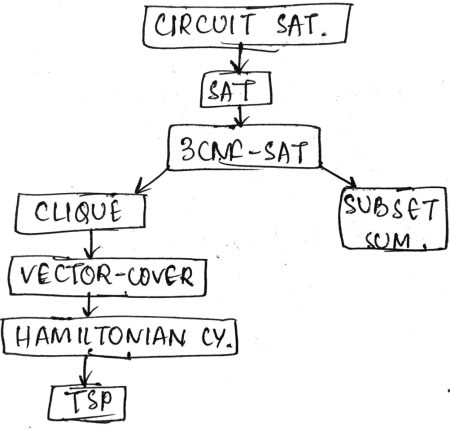
In the diagram, Hamiltonian cycle, TSP and subset sum problems can also be converted into NP-Complete problems.

These are the basic set of NP-Complete problems.